2011-2017 © МБУЗ ГКП № 7, г.Челябинск.
Регистратура:
(351)725-26-73, (351)725-26-72, (351)725-26-89.
Вызов врача на дом: (351)725-22-33, (351)725-51-58.
Неотложная помощь: (351)725-42-08.
Схема проезда
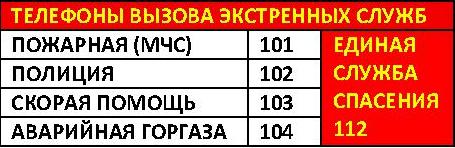
Телефонный справочник
Содержание, карта сайта.
В будни: 7:30 — 20:00 (прием пациентов: 08:00 — 19:00)
В субботу прием ведут: терапевт, хирург, невролог, отоларинголог, окулист в 8:00 - 14:00
Неотложная помощь оказывается ежедневно с 11:00 до 23:00
2011-2017 © МБУЗ ГКП № 7, г.Челябинск.